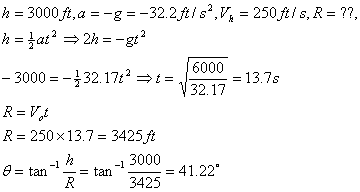GENERAL ORGANIZATION FOR TECHNICAL EDUCATION AND VOCATIONAL TRAINING

RIYADH COLLEGE OF TECHNOLOGY

MECHANICAL TECHNOLOGY DEPARTMENT

ME-392: Mechanics                                                               Fall 1427/1428 (27-2)

HW 5 Solution

 

Problem 12.1: A car starts from rest and reaches a speed of 80ft/sec after travelling 500ft along a straight road. Determine its constant acceleration and time of travel?

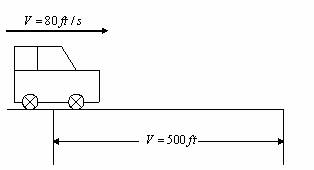
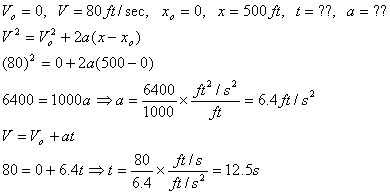Solution:

 

 

 

 

 

 

 

 

 

 

 

 

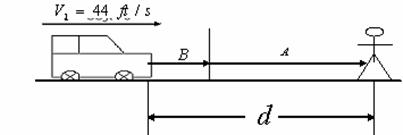
Problem12.5:  Tests reveal that a normal driver can react to a situation in 0.75 sec. before beginning to avoid a collision. It takes about 3 sec for a driver having 0.1% alcohol in his system to do the same. If two such drivers are traveling on a straight road at 30mph (44ft/s) and their cars can decelerate at 2 ft/ sec2, determine the shortest stopping distance d for each from the moment they see the pedestrians at A. Moral: Never drink or take drugs.

 


x2
 

x1
 
Solution:

 

 

x
 
For the normal driver:

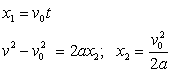
Note that

 

For the drunk driver:

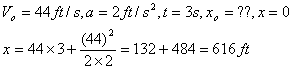
Problem12.18: A motorcycle starts from rest at t=0 and travels along a straight road with a constant acceleration of 6 ft/sec2 until it reaches a speed of 50 ft/sec. Afterwards it maintains this speed. Also, when t = 0, a car located 6000 ft down the road is travelling toward the motorcycle at a constant speed of 30 ft/sec. Determine the time and distance travelled by the motorcycle when they pass each other?

 

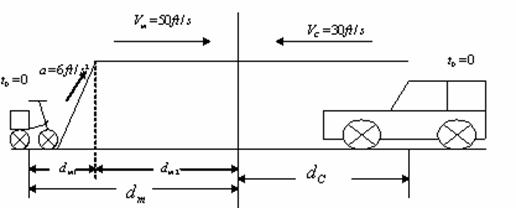
Solution

For the motorcycle

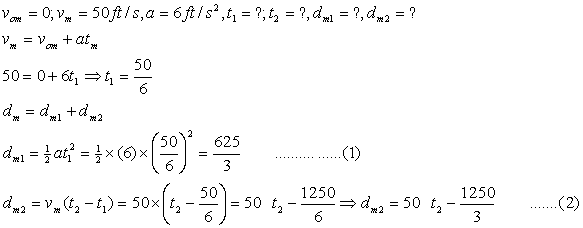
For the car

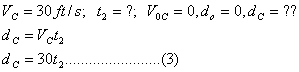
Also, the total distance is 6000 ft:

 

Using equations (1-3) into (4)

 

 

 

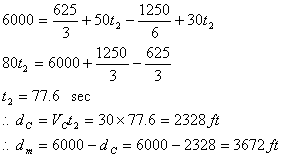
Problem12.59:  The pitcher throws the baseball horizontally with a speed of 110ft/s from a height of 5ft. If the batter is 60 ft away, determine the time needed for the ball to arrive at the batter and the height at which it passes the batter?

 


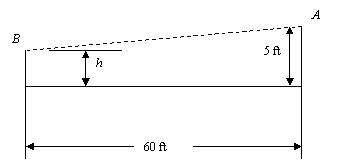Solution

 

 

 

 

 

 

 

 

 

 

 

 

 

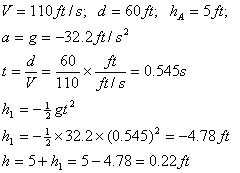
Problem12.66:  The plane is flying horizontally with a constant speed of 250ft/s at an altitude of 3000ft. If the pilot drops a package with the same horizontal speed of 250ft/s, determine the angle q at which he must sight the target B so that when the package is released it falls and strikes the target. Air resistance neglected, explain why the package appears to remain directly beneath the plane as it falls?

 

                  

 

 

 

 

 

 

 

 

 

Solution